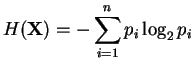Voici un exemple de calcul d'entropie: supposons que ![]() représente
le résultat d'un lancé de pièce de monnaie. La distribution est définie
par
représente
le résultat d'un lancé de pièce de monnaie. La distribution est définie
par
![]() , donc que la
probabilité que
, donc que la
probabilité que ![]() représente l'un ou l'autre des deux éléments
de la distribution est égale. Puisque la seule information que l'on
peut avoir de la valeur de
représente l'un ou l'autre des deux éléments
de la distribution est égale. Puisque la seule information que l'on
peut avoir de la valeur de ![]() est
est ![]() lui-même et que chaque élément
de la distribution a une même probabilité de se produire, l'entropie
sera la longueur, en bits3, de la chaîne4 la plus courte permettant de décrire
lui-même et que chaque élément
de la distribution a une même probabilité de se produire, l'entropie
sera la longueur, en bits3, de la chaîne4 la plus courte permettant de décrire ![]() . L'entropie est de un bit
parce qu'on peut coder
. L'entropie est de un bit
parce qu'on peut coder
![]() par 0 et
par 0 et
![]() par 1. L'entropie d'une chaîne de
par 1. L'entropie d'une chaîne de ![]() lancés de cette même pièce
de monnaie aura une entropie de
lancés de cette même pièce
de monnaie aura une entropie de ![]() bits parce qu'il faudra au minimum
bits parce qu'il faudra au minimum
![]() bits pour la représenter parfaitement, un bit pour le résultat
de chaque lancé.
bits pour la représenter parfaitement, un bit pour le résultat
de chaque lancé.
Supposons maintenant qu'on lance un dé à 4 faces au lieu d'une pièce
de monnaie. Il y a maintenant 4 résultats possibles, chacun ayant
une probabilité de se produire de
![]() . On pourra coder
les résultats comme ceci:
. On pourra coder
les résultats comme ceci:
| 1 | 00 |
| 2 | 01 |
| 3 | 10 |
| 4 | 11 |
On remarque qu'afin de pouvoir représenter chaque résultat, il nous faut une chaîne de 2 bits. L'entropie de cette distribution est donc de 2 bits. La longueur de la chaîne binaire nécessaire pour encoder tous les résultats, et donc de l'entropie en terme de bits, est donnée par l'équation
À probalités inégales, il faudra faire la moyenne des probabilités
pour trouver l'entropie. Une distribution de probabilités
![]() aura une probabilité moyenne de
aura une probabilité moyenne de
![]() . En utilisant la formule
ci-dessus, on trouve une entropie d'environ 1.58 bits. Puisqu'une
chaîne a toujours une longueur entière, une partie de bit sera redondante.
. En utilisant la formule
ci-dessus, on trouve une entropie d'environ 1.58 bits. Puisqu'une
chaîne a toujours une longueur entière, une partie de bit sera redondante.
Un événement de probabilité ![]() peut être codé sur une chaîne
de longueur
peut être codé sur une chaîne
de longueur ![]() . Par exemple, un événement de probabilité
. Par exemple, un événement de probabilité
![]() ,
laquelle peut aussi s'exprimer
,
laquelle peut aussi s'exprimer ![]() , nécessite une chaîne de
longueur 3 pour être représenté. Plus généralement, un événement de
probabilité
, nécessite une chaîne de
longueur 3 pour être représenté. Plus généralement, un événement de
probabilité ![]() peut se coder sur une chaîne de longueur
peut se coder sur une chaîne de longueur
![]() ,
arrondi à l'entier supérieur. Lorsqu'on exprime l'équation ci-dessus
selon les probabilités individuelles de chacun des résultats possibles,
on obtient
,
arrondi à l'entier supérieur. Lorsqu'on exprime l'équation ci-dessus
selon les probabilités individuelles de chacun des résultats possibles,
on obtient