4.1.2 Entropie d'un langage humain

L'entropie d'une lettre dans un texte quelconque, en supposant que l'alphabet comporte 26 symboles, est de $-\log _{2}\left(\frac{1}{26}\right)\approx 4,70$. Ceci est une première approximation, en supposant que toutes les lettres sont générées au hazard. Cependant, il s'agit ici d'un texte réel, et chaque lettre a une fréquence d'appartition indépendante des autres. Par exemple, le « e » est plus souvent utilisé que le « z », comme pourrait l'indiquer un tableau des fréquences d'apparition des lettres dans une langue donnée, lequelle aura été construit à partir de l'analyse de milliers de pages de texte standard. Le tableau 2 est un exemple d'un tel tableau. Grâce à ce tableau des fréquences, on trouve que l'entropie du français $H_{F}$ est d'environ 3,954 bits.

Table 2: Fréquences d'apparition des lettres dans un texte français

Table 2: Fréquences d'apparition des lettres dans un texte français

Lettre	Fréquence	Lettre	Fréquence
	(%)		(%)
A	8,11	N	7,68
B	0,81	O	5,20
C	3,38	P	2,92
D	4,28	Q	0,83
E	17,69	R	6,43
F	1,13	S	8,87
G	1,19	T	7,44
H	0,74	U	5,23
I	7,24	V	1,28
J	0,18	W	0,06
K	0,02	X	0,53
L	5,99	Y	0,26
M	2,29	Z	0,12

L'information fournie par la position d'une lettre dans une phrase et ses relations avec les autres lettres est encore plus grande que la simple probabilité d'une lettre individuelle. Par exemple, un « q » est souvent suivi d'un « u ». L'entropie calculée sur l'ensemble des $26^{2}$ digrammes⁵ possibles devrait donc être plus faible que celle des lettres simples. On peut faire l'approximation que l'entropie de l'anglais claculée selon les digrammes est la moitié de celle calculée selon les monogrammes (voir section 4.1.3 pour des valeurs exactes). On peut étendre cette approximation aux $n$-grammes et définir la distribution $\mathbf{X}^{n}$ de tous les $n$-grammes de texte clair possible dans un langage $L$. Cela donnerait, lorsque $n$ tend vers l'infini,

$$H_{L}=\lim _{n\rightarrow \infty }\frac{H(\mathbf{X}^{n})}{n}$$

On remarque que, dans l'approximation précédente, plus on augmente la valeur de $n$, plus l'entropie diminue.

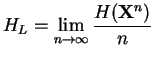
L'entropie est importante en cryptographie. Il est important de tendre vers une entropie la plus grande possible, puisqu'une grande entropie est associée à une grande incertitude sur le texte clair lorsqu'on a déchiffré une partie du texte chiffré. Les techniques modernes de chiffrement produisent un texte chiffré indiscernable d'un texte aléatoire.